P地からQ地へ行くのに、P地を出発して14分間は分速75mで歩き、その後歩く速さを速くして、分速95mで26分間歩いてQ地へ着きました。
(1) P地からQ地まで何mありますか。
(2) このときの平均の速さは分速何mですか。
解答解説はこちら
(1)の答え : 3,520m
下の図のように、P地を出発して分速75mの速さで14分間歩いた道のり(ア)は 75m/分×14分で1,050m、その後Q地まで、分速95mの速さで26分間歩いた時の道のり(イ)は95m/分×26分で2,470mになる。
P地からQ地までの道のりは1,050+2,470で3,520mになる。
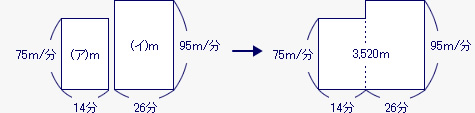
(2)の答え : 分速88m
平均の速さとは、ある地点からある地点まで、速さを変えながら進んだときと同じ時間をかけて、その道のりを一定の速さで進んだときの速さである。
P地からQ地までの3,520mを一定の速さ□m/分で進んで、14+26の40分かかったとすると、このときの速さ、時間、道のりの関係は、次の図のような長方形で表すことができる。
このことより、求める速さは3,520m÷40分間で88m/分になり、これが平均の速さになる。
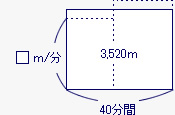
このことより、平均の速さは次のようにして求めることがわかる。
(平均の速さ)=(全体の道のり)÷(全体にかかった時間)
ここで、(75+95)÷2を計算すると85m/分となり、2つの速さの和を求めて2でわっても、平均の速さにはならないことに注意しよう。



