次の問いに答えなさい。
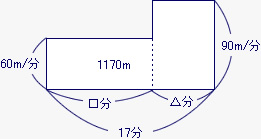
（1） とし子さんは家から公園まで行くのに、途中の郵便局までは分速60ｍの速さで歩き、
そこから分速90ｍの速さに変えて公園まで歩いたところ、全部で17分かかりました。
家から公園までの道のりは1,170ｍです。分速60ｍの速さで歩いたのは何分間ですか。
（2） 5％の食塩水を150ｇと8％の食塩水を何gか混ぜたところ、7％の食塩水ができました。8％の食塩水を何ｇ混ぜましたか。
解答解説はこちら
(1)の答え ： 12分間
分速60ｍで□分、分速90ｍで△分歩いたとすると、全体の歩いた道のりは、下の図の面積図で表される。
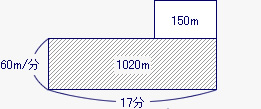
この面積図を下の図のように分けると、斜線部分の道のりは60ｍ/分×17分で1,020ｍになる。
全体の歩いた道のりは1,170ｍだから、 部分の道のりは1,170−1,020で150ｍになる。
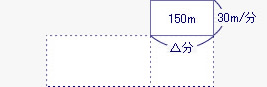
下の図のように 
部分の縦は90−60の30ｍ/分、横は△分間を表すから、分速90ｍで歩いた時間△分は150ｍ÷30ｍ/分で5分になる。
家から公園までは17分かかったから、分速60ｍで歩いた時間は17−5で12分間になる。
(2)の答え ： 300ｇ
下の図のように、5％の食塩水を150ｇと8％の食塩水を□ｇ混ぜると、食塩の重さは二つ目の面積図で表される。
また、このときの食塩水の濃度0.07は、面積図の縦で表される。
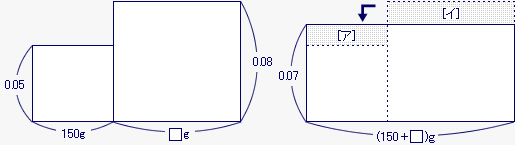
上の二つの図を比べたとき、全体の食塩の重さは同じだから、二つ目の図の[ア]と[イ]の食塩の重さは等しいといえる。
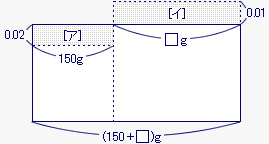
上の図の[ア]の縦は0.07−0.05の0.02、横は150ｇを表すから、[ア]の食塩の重さは150ｇ×0.02で3ｇになる。
[イ]の縦は0.08−0.07の0.01だから、8％の食塩水は3ｇ÷0.01で300ｇになる。
