次の問いに答えなさい。
(1) 映画館に、大人3人と子ども4人で入ると、入場料は10,000円いります。
また、大人2人と子ども3人では7,000円いります。
大人1人、子ども1人の入場料はそれぞれいくらですか。
(2) 6km離れた道のりを、途中までは時速2kmで歩き、残りを時速12kmで走ると、
全部でちょうど1時間かかりました。
歩いた時間と走った時間をそれぞれ求めなさい。
解答解説はこちら
(1)の答え : 大人…2,000円 子ども…1,000円
映画館の大人1人の入場料を□円、子ども1人の入場料を△円として面積図に表すと、大人3人と子ども4人で入った場合は上の図、大人2人、と子ども3人で入った場合は下の図になる。
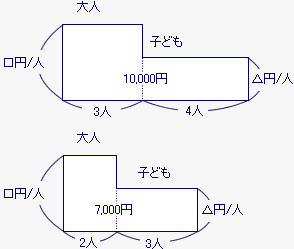
二つの図を比べると、大人の人数も子どもの人数も違うので、どちらかの人数をそろえて考える。
大人の人数をそろえる場合を考えると、3人と2人なので、両方を何倍かしてそろえる。このようなときは、2つの数の最小公倍数にそろえる。3と2の最小公倍数は6だから、大人の人数を6人にそろえて考える。
大人3人と子ども4人を1組として、2組入ったとすると、大人は3×2で6人、子どもは4×2で8人、入場料は10,000×2で20,000円になる。
また、大人2人と子ども3人を1組として、3組入ったとすると、大人は2×3で6人、子どもは3×3で9人、入場料は7,000×3で21,000円になる。それぞれの場合を面積図に表すと、下の図のようになる。
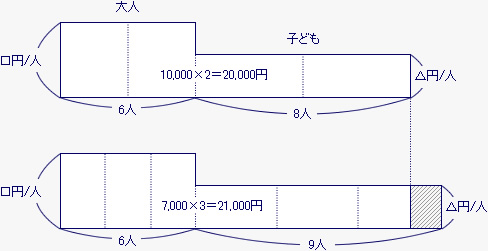
2つの面積図を比べると、大人の人数は同じだから、9−8で子ども1人分の入場料が、21,000−20,000で1,000円になることがわかる。大人2人と子ども3人で7,000円だから、大人2人の入場料は7,000−1,000×3で4,000円になる。大人1人の入場料は4,000÷2で2,000円になる。
(2)の答え : 歩いた時間…0.6時間 走った時間…0.4時間
このときのようすを面積図に表すと、下の図のようになる。
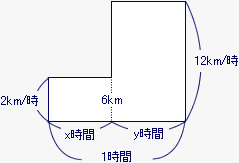
まず、歩いた時間x時間と走った時間y時間の合計が1時間だから、x+y=1になる。
次に、全体の道のりを考える。時速2kmでx時間歩いたから、歩いた道のりは2x(km)になり、時速12kmでy時間走ったから、走った道のりは12y(km)になる。
だから、全体の道のりは6kmなので、2x+12y=6になる。
このことから、xとyについて、次の2つの式をつくることができた。
![]() x+y=1 …… [1]
x+y=1 …… [1]
2x+12y=6 …… [2]
xをそろえるために[1]の式を2倍すると、次のようになる。
2x+2y = 2 …… [3]([1]×2)
2x+12y = 6 …… [2]
2xが同じなので[2]の式から[3]の式を引いてyを求める。
(12−2)y= 6−2
10y = 4
y = 0.4
y=0.4を[1]の式にあてはめて、xを求める。
x+0.4 = 1
x = 1-0.4
x = 0.6
x=0.6、y=0.4だから、歩いた時間は0.6時間、走った時間は0.4時間になる。


