周囲が600mの池の周りを、分速65mの速さで歩くあきら君と、分速50mの速さで歩くよし子さんが、同時に同じ所を出発して、同じ方向にまわります。
(1) あきら君がよし子さんに初めて追いつくのは、出発してから何分後ですか。
(2) あきら君が3回目によし子さんに追いつくのは、出発してから何分後ですか。
解答解説はこちら
(1)の答え : 40分後
1分後、2分後、3分後、…と時間がたつにつれて、2人は次の図のようにだんだんはなれていき、あきら君がよし子さんに初めて追いついたとき、あきら君はよし子さんよりちょうど池のまわりを1周分多く歩いたことになる。
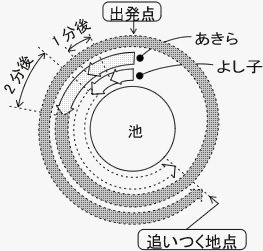
x分後に初めて追いつくとすると、x分間にあきら君とよし子さんが歩いた道のりは、それぞれ下の図のような面積図に表せ、この道のりの差が池のまわり1周分の600mになる。
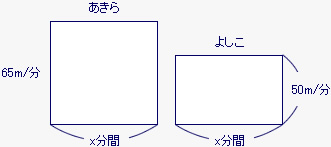
この問題も2つの面積図の差を考えるので、下の図のように面積図を重ねて考えるとよい。
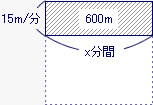
下の図の斜線部分の縦は65−50で15m/分、横はx分、面積は600mを表すので、x分は600÷15m/分で40分になる。
(2)の答え : 120分後
あきら君がよし子さんに追いついた地点を出発点と考えると、あきら君は再び40分後によし子さんに追いつくので、40分の倍数の時間ごとに追いつくことになる。
3回目に追いつくのは、40×3で120分後になる。


