時速5kmの速さで流れている川があります。静水時の速さが時速10kmの船がこの川を往復します。
(1) 川を3時間下ったとき、この船は川を何km下りますか。
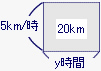
(2) この船は川を20km上るのに何時間かかりますか。
解答解説はこちら
(1)の答え : 45km
川の水の流れの速さを調べるには、例えば、川に木の葉をうかべて、木の葉が下流へと動いていく速さで調べることができる。これは、木の葉が水の運んでいく力によって、流れる水と同じ速さで動くからである。
また、船のようにそれ自身が動くものであれば、水も船も動くから、水と船それぞれの動く速さと方向をかんがえなければならない。
船が川を下る場合は、川の流れと同じ方向に船は進む。まず、水の流れがないと考えて、船が自分で進む道のりを考えよう。この船の静水時の速さ(水の流れがないところで、船が進む速さ)は時速10kmだから、次の図の<1>の矢印の方向に、1時間あたり10km進む。
次に、船が止まっていると考えて、川の水が船を進める道のりを考えよう。この川の流れの速さは時速5kmだから、図の<2>の矢印の方向に、川の流れは1時間あたり5km進む。
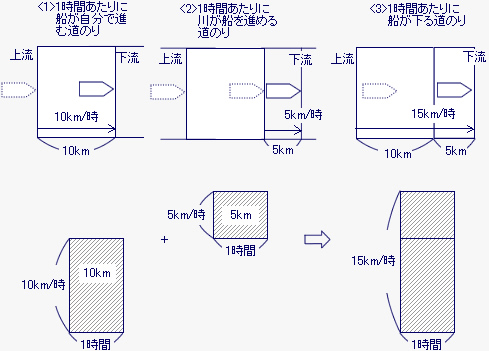
船が川を下るとき、船は川と同じ方向に進むから、1時間あたりに船が川を下る道のりは、船が自分で進んだ道のり10kmと、水が船を進めた道のり5kmとの和に等しく、10+5で15kmになる。船が川を下るときの速さは時速15kmである。
このように、船が川を下るときの速さは、船の静水時の速さと川の流れの速さとの和になる。
(川を下るときの速さ) =(船の静水時の速さ)+(川の流れの速さ)
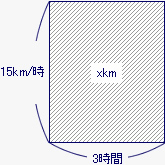
この船が時速15kmの速さで川を3時間下ったときに進む道のりをxkmとして面積図に表すと、下の図のようになる。川を下った道のりxkmは15×3で45kmになる。
(2)の答え : 4時間
船が川を上る場合は、川の流れと反対の方向に船は進む。まず、水の流れがないと考えると、この船の静水時の速さは時速10kmだから、次の図の<1>の矢印の方向に、1時間あたり10km進む。
次に、船が止まっていると考えると、川の流れの速さは時速5kmだから、川の流れは図の <2>の矢印の方向に、1時間あたり5km進む。
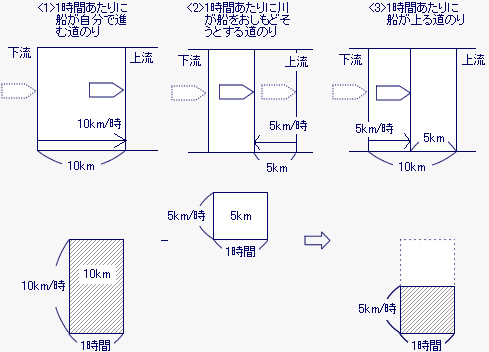
船が川を上るとき、船は川と反対方向に進むから、川の流れが船をおしもどすことになり、1時間あたりに船が川を上る道のりは、船が自分で進んだ道のり10kmと、水が船をおしもどした道のり5kmとの差に等しく、10−5で5kmになる。船が川を上るときの速さは時速5kmである。
このように、船が川を上るときの速さは、船の静水時の速さと川の流れの速さとの差になる。
(川を上るときの速さ)=(船の静水時の速さ)−(川の流れの速さ)
この船が時速5kmの速さで川を20km上ったときにかかった時間をy時間として、面積図に表すと、次の図のようになる。かかった時間y時間は20÷5で4時間になる。