次の問いに答えなさい。
(1) 15kmの道のりを往復するのに、行きは時速3kmで、帰りは時速5kmで歩きました。
往復の平均の速さは時速何kmですか。
(2) 自転車で家から駅まで行くのに、最初の15分間は分速400mの速さで走り、その後は
分速300mの速さで走りました。家から駅までの平均の速さは分速360mでした。
分速300mの速さで走ったのは何分間ですか。
解答解説はこちら
(1)の答え : 時速3.75km
速さは普通、途中で速くなったりおそくなったりする。平均の速さとは、ある道のりを一定の速さで進んだものとして考えたときの速さのことで、次の式で求められる。
(平均の速さ)=(全体の道のり)÷(全体にかかった時間)
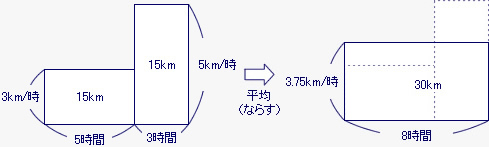
行きは、15kmを時速3kmで歩くので、15km÷3km/時で5時間かかる。
帰りは、15kmを時速5kmで歩くので、15km÷5km/時で3時間かかる。
全体の道のりは15+15で30km、全体にかかった時間は5+3で8時間だから、平均の速さは30km÷8時間で3.75km/時になる。
(2)の答え : 10分間
分速300mでx分走ったとすると、家から駅までの全体の道のりは下の左の面積図に表される。
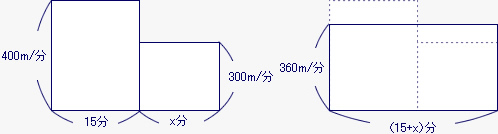
このでこぼこをならして考えたものが平均の速さなので、それは上の右の図の長方形の縦で表される。上の二つの図は面積(全体の道のり)が等しいので、下の図の斜線部分[ア]と[イ]の面積は等しくなる。
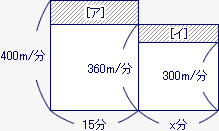
[ア]の縦は400−360で40m/分、横は15分を表しているので、[ア]の面積は40m/分×15分で600mになる。
[イ]は縦が360−300で60m/分、横がx分、面積が[ア]と等しい600mなので、x分は600m÷60m/分で10分になる。


