4、7、10、13、16、……のように、ある規則にしたがって並んでいる数があります。
(1) 4から数えて30番目の数は何ですか。
(2) 4から20番目までの数を全部たすと、いくつになりますか。
解答解説はこちら
(1)の答え : 91
この数の列は、4から始まって3ずつ増えるという規則にしたがって並んでいる。
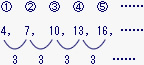
このようにとなり合う2つの数の差が等しいとき、N番目の数は、最初の数+差×(N−1)という式で求められるから、30番目の数は4+3×(30−1)で91になる。
(2)の答え : 650
20番目の数は4+3×(20−1)で61になる。
4+7+10+13+…+49+53+57+61の答えをxとすると、xは次のように、たす順序を逆にした式を加えて考える。
![]()
65を20個たした数がxのちょうど2倍になるので、4から61までの数の和は(4+61)×20÷2で650になる。
このように、差が等しい数の列でN番目までの数の和は、(初めの数+終わりの数)×個数÷2で求めることができる。


