次の問いに答えなさい。
(1) 4、6、9、13、18、24、……のように、ある規則にしたがって並んでいる数があります。
4から数えて15番目の数は何ですか。
(2) 次のように、ある規則にしたがって並んでいる数があります。左から50番目の数を求めなさい。
1、2、2、3、3、3、4、4、4、4、……
解答解説はこちら
(1)の答え : 123
この数の列は、4から始まってとなり合う2つの数の差が2、3、4、5、6、…と1つずつ増える規則にしたがって並んでいる。
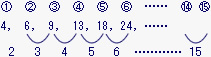
15番目の数までに、となり合う2つの数の差は15−1で14個あるから、もとの数の列の14番目の数と15番目の数は2+1×(14−1)で15はなれていることがわかる。
1番目の4と15番目の数との差は、2+3+4+……+13+14+15=(2+15)×14÷2で119になる。
15番目の数は4+119で123になる。
(2)の答え : 10
この数の列は、次のように区切って考える。
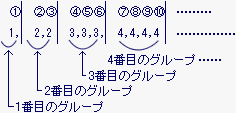
この数の列は、(1)、(2、2)、(3、3、3)、(4、4、4、4)、…と、1から順に1番目のグループは1が1個、2番目のグループは2が2個、3番目のグループは3が3個、4番目のグループは4が4個、…とグループをつくって並んでいることがわかる。
1から10までの数の和は55だから、1番目のグループから10番目のグループまでに55個の数がある。
10番目のグループには10が10個ふくまれているから、左から50番目の数は10になる。


