次の問いに答えなさい。
（1） 1、2、3、4、5の5個の数字があります。同じ数字を1度しか使えないとして3けたの整数をつくるとき3で割り切れる整数は何個ありますか。
（2） 4枚のカード
、
、
、
があります。これらのカードから2枚のカードを取り出す方法は何通りありますか。
解答解説はこちら
(1)の答え ： 24個
3で割り切れる整数（3の倍数）の各位の数の和は3の倍数になっている。例えば3の倍数である123で考えると、123の各位の数の和は1＋2＋3の6で、3の倍数になっていることがわかる。
百の位が1のときを樹形図に表すと、次のように3けたの整数は12通りできる。
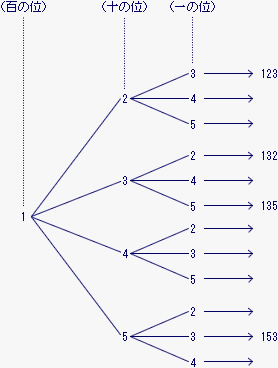
このうち、各位の数の和が3の倍数になっている整数は123、132、135、153の4個である。
同じように樹形図を使って考えると、百の位が2のときは213、231、234、243の4個、百の位が3のときは312、315、321、324、342、345、351、354の8個、百の位が4のときは423、432、435、453の4個、百の位が5のときは513、531、534、543の4個ある。
1、2、3、4、5の5個の数字を使ってできる、3けたの3の倍数は4＋4＋8＋4＋4で24個ある。
(2)の答え ： 6通り
4枚のカードから2枚のカードを取り出して並べる方法を樹形図に表すと、次の図のように全部で12通りある。
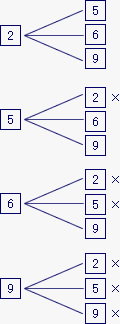
しかし、ここではカードの並べ方を考えるのではなく、カードを取り出す方法を考えるので、例えば、とは同じ2枚のカードを取り出したことになる。これは1通りと考えるので、このような場合を除くと、取り出す方法は全部で6通りになる。
