次の問いに答えなさい。
(1) 5円、10円、100円、500円の硬貨が1枚ずつあります。これらの硬貨を使って払うことができる金額は全部で何通りありますか。
(2) 10円玉、50円玉、100円玉を何枚か使って、420円の買い物をしておつりがないように払います。
どの硬貨も必ず1枚は使うとすると、お金の払い方は全部で何通りありますか。
解答解説はこちら
(1)の答え : 15通り
4枚の硬貨から1枚使う場合、2枚使う場合、3枚使う場合、4枚使う場合に分けて考える。
[1] 4枚の硬貨から1枚の硬貨を使う方法
1枚を使って払うことのできる金額は5円、10円、1,000円、500円の4通りである。
[2] 4枚の硬貨から2枚の硬貨を使う方法
金額が同じになる場合を除いて樹形図に表すと、下の図のように6通りある。
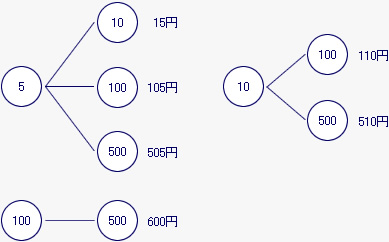
[3] 4枚の硬貨から3枚の硬貨を使う方法
5円硬貨を必ず使うときを樹形図に表すと、下の図のように3通りある。
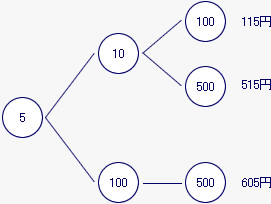
また、5円硬貨を使わないときは、10+100+500で610円の1通りだけだから、4枚の硬貨から3枚の硬貨を使って払うことができる金額は3+1で4通りある。
[4] 4枚の硬貨全部を使う方法
払うことができる金額は5+10+100+500で615円の1通りある。
[1]〜[4]より、1枚の硬貨を使う場合が4通り、2枚の硬貨を使う場合が6通り、3枚の硬貨を使う場合が4通り、4枚の硬貨を使う場合が1通りだから、全部で4+6+4+1の15通りになる。
(2)の答え : 12通り
100円玉を基準にして、100円玉をいちばん多く使う場合から順序よく表をつくって考えていく。
420円の買い物をするとき、100円玉は一番多くて4枚使える。しかし、このとき残りの代金は420−400の20円で、この金額は10円玉でしか払えない。これでは50円玉を使わないことになってしまい、どの硬貨も必ず1枚は使うという条件にあてはまらないので、100円玉は一番多くて3枚しか使えないことがわかる。
100円玉を3枚使ったとき、残りの代金は420−300の120円で、この金額を50円玉と10円玉で払う方法を考える。このときも、50円玉をいちばん多く使う場合から順序よく考えていく。
このようにして、100円玉の枚数を2枚、1枚と減らしていくと、お金の払い方は次の表のようになる。
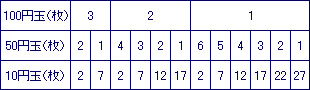
上の表より、お金の払い方は全部で12通りである。


